The Cubic Atomic
Model
You are vistor
I have discovered an elegant and simple way to describe what may be the actual
mechanical structure of atoms. It is so simple that even a child could grasp
it. I orginally discovered and visualized this atomic model by using Lego Duplo building blocks which is a simple
childrenís toy. I call this the Cubic atomic model since this model builds out based on cubes. This mechanical model appears to accurately describe some of the energy
levels for the electron shells and why the exist in the way that they do and it
predicts the location of some of the noble gas elements. The actual structure of an
atom and the electron shell configuration can be explained if we assume that
atoms are assembled like simple proton/electron building blocks using some
simple geometric principles.
**********HOLD THE PRESSES ****************
I have just released a major revision to the Cubic Atomic model. I have taken
into account the electron orbital shells and have revised the model to correctly
account for the energy levels seen. See it at:
http://franklinhu.com/atmpics2.html
Please note: The following theories are purely speculative and largely contradict conventional science!
This theory
of atom construction is presented as something to be considered as one way of explaining the nature of atoms in a more
intuitive way than is described by conventional physics. The primary motivation for the cubic model is to find a way to
describe the construction of the atom without leaving conventional classical mechanics. This is the viewpoint that the
particles that make up the atoms act like objects we see in everyday life like marbles and billiard balls. I make no claim
that this theory is correct. In fact, the chances are, it is completely wrong and may simply serve as an example of how to
create an alternate theory of atom construction that does not rely on our usual notions of electrons orbiting a nucleus. I
have done work to show that can explain some experimental results, but until somebody does experiments which would show
conventional theory wrong and the cubic model as correct, this will remain an untested theory. However, there is still a chance
that this theory is correct. If it were correct, it would significantly change how we view the atom. Therefore, I would invite
people to consider this theory and see if it explains things that conventional theories cannot.
The cubic atomic theory asserts that atoms are constructed according to some simple principles. These should be
considered as guidlines and not hard and fast rules. These principles of construction are:
1.) A protons and electrons must be arranged in a matrix such that
similar particles never touch one another. This is similar to the cubic NaCl salt structure.
2.) The smallest unit that can be added to build an atom is a
combination of 2 electrons and 2 protons (with the exception of Helium). One electron/proton pair can be
considered to be a neutron. The extra proton is bound to the neutron while the
extra electron can be ionized from the atom.
3.) The atom must be constructed to take a minimum of space and be
as symmetric as possible.
4.) The atom consists of a vertical core surrounded by four arms
arranged like the 4 sides of a cube.
5.) All available space must be taken up on the arms before
anything can be added to the vertical core.
6.) Isotopes of an atom are formed by placing additional
neutrons between the arms.
Following these simple geometric rules, you can build models of
atoms using simple building blocks. I have used black and red cubes in
the following series of photographs. The red cubes are protons and the black
cubes are electrons. The white cubes are not part of the model, they just
hold up other parts.

The simplest atom is Hydrogen consisting of a proton and electron.
This could also be the shape of a neutron, however, a neutron and hydrogen behave
very differently. The cubic model attributes this difference to a different and
currently unexplained kind of binding. There are other theories of how a neutron
is constructed (like out of quarks). One of these theories may explain how a
neutron is built. The cubic model would imply that a neutron is about the same
size as a hydrogen atom, although this may not necessarily be the case.

Atoms build up by adding a minimum atomic unit of 2 protons and electrons.
Helium is the exception to the rule in that we need to add 3 protons and electrons in order
to get the correct atomic weight. We get a
cube shape for Helium. Notice the atom is symmetrical about all axes.

Adding another atomic unit, we get Lithium, which looks like a
stack.

Adding a fourth unit, we get Beryllium. At this point, we could
add the 4th atomic unit anywhere on the side instead of stacking them
all up as shown here. But that would seem to be a lobsided arrangement. The
ionization energy data would seem to indicate that there are 2 electrons
with low ionization energy and 2 electrons with high ionization energy. This
would be consistent with a stack, whereby the inner electrons take more energy to
ionize.

We cannot keep building vertically and keep to a minimum size, so
now we must add to the sides to form Boron. Note that the white cubes are not
part of the model, they are just holding up the fifth atomic unit in its position
about the vertical core of the atom.
 Carbon
Carbon
 Nitrogen
Nitrogen
 Oxygen
Oxygen
Carbon, Nitrogen, and Oxygen are formed in a similar manner
filling up the four sides. The atomic units on the side make up the arms of the
atom, while the four center units make up the central vertical core.

We must now build up by adding a unit to the vertical core to
produce Fluorine

Adding another unit to the core produces the nobel gas Neon.
 Sodium
Sodium
 Magnesium
Magnesium
 Aluminium
Aluminium
 Silicon
Silicon
Because the vertical core is tall enough, we can now place two
atomic units on each arm of the atom. Adding another atomic unit, we can
Sodium. If we continue to add to the other arms, we get Magnesium, Aluminum and
Silicon .
 Argon
Argon  Color coded cross section of Argon
Color coded cross section of Argon
The outer sides of Silicon are tall enough to allow another unit
to be attached to the sides to produce Phosphorus, Sulfur, Chlorine and Argon.
This picture shows an Argon atom and and a color coded cross section view of an Argon atom where
you can clearly see the central core and the arms. There are six outer electrons and the second electron shell is
shown starting with the green core. All of the 8 electrons surrounding the core
would presumably have the same energy level and the red core represents the 2
electrons in the first shell.
 Krypton
Krypton
Adding on 2 more units to the core and fully populating one of the
arms, we come to the noble gas Krypton. Each of the arms contains 7
units X 4 sides = 28 units for the arms + 8 units in the core = 36 total units.
This atom is not fully symmetric since the arms have an extra atomic unit
protruding from the sides, but was required to get the correct number of
electrons for Krypton. The matching up of the electron shells is not completely
clear, but appears to roughly approximate what we see.
 Xenon
Xenon
Adding on 2 more units to the core and fully populating
the arms we get the noble gas Xenon at 54 electrons. There are 11 electrons in
the arms (total of 44) and 10 electrons in the core. I have only shown half of
the atom since the backside is identical to the front side.
 Hafnium
Hafnium
Expanding this by adding 2 more units to the core, we get Hafnium at 72
electrons. Interestingly, this is not the next nobel gas, so there is a break in the
geometric sequence. Some other rule must apply past Xenon.
 Californium
Californium
Adding 2 more units to the core, we get Californium at 98. I have only shown
the core and one of the arms since the other arms will look the same. This isn't a noble gas
either. The nearest noble gas is Radon at 86. How do we resolve this problem?
The difference in atomic number between Californium and Radon is 98-86 = 12.
If we believe that the difference is going to be in the arms of the atoms, this
means that each arm (4 of them) have 3 too many electrons. So this means we have
to remove 3 electrons from each arm of Californium. It turns out that there are
3 electrons in the outer most arms of Californium and if we remove them, we get:
 Radon
Radon
What is interesting to note about this atom is that it is entirely constructed of
helium nuclei which is a cube composed of 4 protons and 4 neutrons.
Click here to view pictures of all atoms Hydrogen to Xenon
What does the cubic model help explain?
Having a simple atomic model is great, but it is only as good as what it helps
to explain. Here are some things that the cubic model can help explain.
The reactivity of an atom is related to symmetry
It is curious that the reactivity of an atom appears to be loosely tied to symmetry, but in the case of noble gases, a protruding unit doesn't make it more reactive and some perfectly symmetric atoms like Oxygen are very reactive. I couldn't figure out why this was until I was forced to tape together my cubes into groups of 8 which is basically a helium atom. Otherwise, I was unable to stack more than 8 cubes before my model started to fall over. You could say my model lost stability if it wasn't grouped into larger units. I discovered that the reason why there is a protruding atomic unit in the arms is to allow it to be made up of whole helium atoms. There seems to be a loose relationship between at atom being made up of helium atoms and being a noble gas. The rule is loose because Krypton and Xenon contain significant non-helium components. Hafnium may not be a noble gas since the core would actually need an odd number of helium atoms to be made up of only helium atoms. This is because to start with a center helium atom and then you must add a helium to the top and bottom to remain symmettric. If you look at Radon, it contains an odd number of helium atoms in the core. There do appear to be some inconsistencies in the relationship between the atom structure and whether it is a noble element. This is an area of further study.
Why the electron shell energy levels are arranged in the way that they are
The cubic model can help explain the atomic electron shell
configurations. Here is a chart of the electron shells and their
relative energy level (from www.welements.com).

You will notice a striking pattern of repeating energy levels.
Each of the 7 primary electron shells is like an inverted pyramid. And one noble
element is found in each shell. Why should it be arranged like this? Lets
examine this in light of the Cubic atomic model we are building.
You can imagine that if you shake a cubic atom by adding energy to
it, some electrons will be looser than others. The electrons on the outside
would take less energy to ionize than electrons contained in the vertical core.
Neon has 3 energy levels shown in the electrons shells 1 and 2. The first 2 electrons
contained in the center of the core match the 2 electrons in Neon's first
electron shell. The next 2 electrons in the core (which you can see poking up
above the arms of the atom), represent the 2 electrons contained in the 2nd
energy level. The six outermost electrons represent the six electrons in the
third energy level. This simple mechanical model shows why we see a triangular
pattern in the electron shells. At the bottom of the triangle are the electrons
in the vertical core and these start the basic electron shell. The reason why
we have six electrons in the outermost shell is because a cube has six faces
and atoms form using a cubic geometry around the 2 central atomic units. The
number of electrons in the next higher energy level are in groups of four
(because of the four sides of a cube), plus 2 extra electrons in the vertical
core. Lets go on to heavier elements.
Explains where neutrons are contained in the atom and why they don't contribute
to the chemical properties
It is also
interesting to note that the atom builds up narrow arms instead of filling in
the spaces between the arms. This was also required to get the correct energy
levels and number of electrons. However, we know that the larger atoms can take
additional neutrons to form isotopes. I would think that the neutrons fill in
the spaces between the arms. Since they are effectively sheilded by the extended
arms, they do not have an effect on the chemical bonding properties of the atoms.
Small atoms like Silicon have very short arms and can only take a few extra
neutrons. Large atoms like uranium with long arms can take many more neutrons.
This is an area of further study to see if there is a specific relationship
between the size of the arms and the number of neutrons an atom can take.
Eliminates the problem of why should an electron orbit the nucleus
This model of the atom is indeed very simple and we can see why
there is a geometric regularity to the electron energy shells as the atom is
built up. If we take this model as being the true structure of atoms, it would
answer a couple of big problems with existing traditional atomic models which
assume that electrons orbit around the nucleus. The most prominent of these
problems is that if an electron orbits, it must expend energy and must
eventually fall into the nucleus. The Cubic model solves this problem by simply
placing the electrons in a fixed matrix within the atom. You would have to give
up the cherished notion that electrons orbit like little planets around the
nucleus Ė but I donít know of any real empirical reason why it should be like
this and this was abandoned long ago in favor of the quantum mechanical view
that the electron isn't a particle at all, but it is a probability cloud described
by a wave equation. This model also explains why electrons have very specific energy levels
when they are jumping between levels. The electrons simply fall into different
slots which are a fixed distance away from the core of the atom. The model
would also explain how is it that electrons in the core can escape and be
ionized, because if an atom has 4 protruding arms, the electrons are never far
from free space and donít have to make their way through other electron shells
to escape.
Eliminates the need for a strong nuclear force.
Since all of the protons and neutrons are not packed into a dense speck in the
middle of the atom, there is no need to presume that there must be some extremely
strong force holding them in there. The cubic model allows the atom to be a
balanced neutral matrix which can hold together with only normal electrostatic
forces.
Explains the newest pictures of atoms using STM
Another intesting piece of evidence is that scanning tunneling microsopy (STM) has gotten good enough to image the structure of individual atoms. See http://arxiv.org/PS_cache/cond-mat/pdf/0305/0305103.pdf
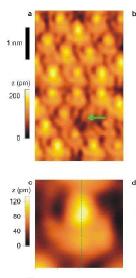
This is an ultra high resolution picture of the surface of silicon atoms. The article
that this picture comes from wants us to believe that we are looking at lobes
of an electron orbital according to quantum mechanics. But what do we really see?
According to the Cubic model, Silicon has a top/bottom atomic unit sticking out above
the atom arms. Look at the picture for silicon. The picture appears to show an arrangement like this.
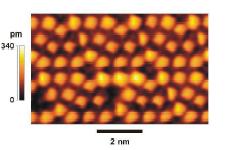
Here is another picture. The tops of the atoms appear to be square, not circular.
The squareness is clearly resolved in the photo and could not correspond to a
smooth wave function or cloud of electrons. Could this squareness be the same as in the Cubic model?
Explains the most common fission products of uranium
Another interesting aspect to consider about the cubic model is what it might say about nuclear fission. If you imagine breaking apart an atom which has the X shape, you would think that it would most likely break off one or more of the arms. I would predict that the most common fission products should be a combination of the core plus parts of the arms. Doing a further analysis on uranium with an atomic number of 92, my model would predict that the core would contain 14 atomic units (a square of electron,proton,neutron) in the core and the arms would contain 19-20 units in each of the arms for a total atomic weight of 92. I would predict that the fission products should contain the core plus parts of the arms. So you would expect to see a 1/4 fraction at 14+20 = 34, 1/2 fraction at 14 + 40=54, 3/4 fraction at 14 + 60 = 74.
The experimental results show the most common fission products being Br,
Kr and Rb at atomic weights 35, 36, 37 and I, Xe, CS at atomic weights
53, 54 and 55. This result can be found in the link:
http://www.chem.uidaho.edu/~honors/decay.html.
This closely corresponds to the predicted 1/4 and
1/2 fractions. The predictions are in the bottom of the range, and I don't
know if there is a match for the 3/4 fraction since that data was not
included, but I think there is a remarkable match between the prediction
and the result. This is significant because you might intuitively think that an atom
should split in half evenly, so that the most common result should be
Palladium at atomic weight 46. But this doesn't happen. We get a lobsided
result which is a little more than 1/2 or 1/4 of the atom. The cubic model
precisely describes why you should get the fractions that we do see in
experiments.
Explains how an alternating series of protons and electrons are stable and why helium is so stable.
To determine if a group of alternating protons and electrons could be stable, I made a calculation to
determine the nature of the forces that would be involved in such a structure. By using nothing more
than Columbs law and geometry, I determined whether the protons/electrons would fly apart or stick
together. A single proton and electron would obviously stick together and be stable since the are
oppositely charged. I then calculated the forces in a square of 2 protons and 2 electrons. All forces
indicated that there was a net inward force to keep it stable. Next I calculated the stability of
a cube of 4 protons and 4 electrons. This too showed a net force pointing toward the center of the
cube that would keep this structure stable. I also calcualated what would happen if you added another
square of 2 protons and 2 electrons, and this also was stable. Based on my calculations, I would say
that the cubic model represents a stable configuration and would not immediately break up. The details
of this calculation can be found at the newsgroup posting:
http://groups.google.com/groups?q=g:thl2147039721d&dq=&hl=en&lr=&ie=UTF-8&oe=UTF-8&selm=46484c9f.0402092244.60bf0487%40posting.google.com&rnum=40
It correctly predicts the relative difference for the first ionization energies for hydrogen and helium
Here is another interesting result of the stability calculation is that it appears
to correctly predict the relative first ionization energies for
Hydrogen and Helium. If we calculate the net force on an element of a
hydrogen atom (just a proton/electron pair at 187pm, we get 3.314 X
10^-9. If we do a similar calculation using the x,y,z forces for an
element of the cube helium, we come up with 5.504 X 10^-9. This
compares with the first ionization energy of hydrogen at 1312 kJ mol
and 2372 kJ mol for helium (from www.webelements.com). The ratio for
the predicted difference in force is (5.504/3.314) = 1.66. The actual
ratio is (2372/1312) =1.80 which agrees to within 9%.
Note that this calculation is only determinining the relative difference
in ionization energy. It does not predict the actual ionization energy.
This is assuming that the ionization energy is related to how tightly
bound the electron is to the rest of the atom. So the more tightly
an electron is bound (with greater force as shown in the calculation),
it should have a higher ionization energy which I have presumed as being
proportional to the force. (A lot of assumptions, not necessarily true.)
This doesn't extend to lithium which would have a force of either
7.696 x 10-9 for an outside component or 2.974 x 10-9 for an inside
component. The first ionization energy for lithium is only 520 kJ mol.
The ratios are (3.313/2.974) = .83 and (1312/520)=2.52 which do not
agree at all. Since this is a completely asymmetric atom, there may be
other factors which make an accurate calculation difficult.
It correctly predicts the relative ionization energies for the remaining electrons in an atom
If you look
at the ionization energies for an atom like argon:

You will notice that there are natural breaks in the energy levels.
The first six have about the same energy difference (about 1000). They do not
have the same ionization energy because as you remove electrons, the
remaining electrons are more tightly bound. This corresponds
to the six faces of a cube which make up the outer layer of argon.
Then there is a grouping of 2 for the 7th and 8th ionization. You can see
that there is a greater amount of energy difference (about 2000) to ionize the 7th and 8th
electron. This
potentially represents the ionization of the next lower layer of the
core of the cubic atomic model. The next 8 ionizations represent the 8
electrons directly surrounding the core. The last 2 represent the very
center core electrons. See the picture of argon:

This is a cutaway, so you can view the atoms core:

You can see that the cubic atomic model gives a reasonable explanation
for the differences in ionization energies and when they occur.
It can roughly explain the results of the Rutherford scattering experiment
One of the main reasons why we believe that the atom consists of a compact nucleus containing
all of the protons and neutrons is the results of the Rutherford scattering experiment.
This experiment shot alpha radiation at a thin flim of gold. Most of the radiation passed
through the gold, but some got reflected at high angles. Rutherford created a formula based
on the idea that the nucleus was small and was able to account for these high angle reflections.
Until now, no one has shown an atomic model that can come close to accounting for these
results, so we presume that Rutherford was right. But I have made a fairly involved calculations
of how the cubic atomic model would perform in this situation and it roughly approximates
the Rutherford experimental results which show that most of the alpha radiation passes straight
through, while a tiny fraction gets reflected at high angles. The details of this calculation
are discussed at the newsgroup post:
I have only just begun to investigate the implications of this
discovery. Certainly, this model should lead to testable predictions and some
of the observations we have already seen may make more sense in light of this
model. As far as I can tell, this theory has never been presented before.
Please send me email to let me know what you think at franklinhu@yahoo.com. This web page will
be updated to reflect what I learn. To see other theories that I am working on,
see the page http://franklinhu.com/gravity.htm
which largely relates to electro-gravity theories. If you'd like to know more about me, see my
main website at: http://franklinhu.com
I have also been debating the issues in the sci.physics newsgroups. So far I have
discovered that I need to explain some of the experimental results like the spectrum
of hydrogen, and Rutherford scattering. But so far, I have not seen any objections that would make this
model impossible. Click here to see the discussion:
news:46484c9f.0401151015.438ea93a@posting.google.com
http://groups.google.com/groups?hl=en&lr=&ie=UTF-8&oe=UTF-8&selm=46484c9f.0402241318.68766535%40posting.google.com