How the magnetic field works

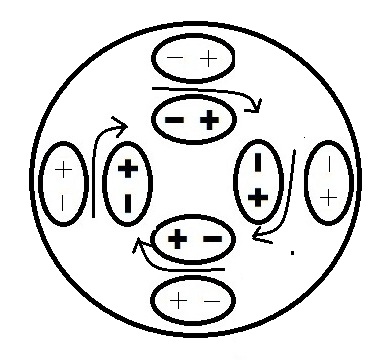
The magnetic field is due to the alignment or linear polariztion of dipole particles called poselectrons. The poselectron simply consists of a bound positron and electron. These dipoles are combed into the same direction by the action of electrons passing through the poselectron sea. This is similar to how a set of compasses could be made to point in the same direction by passing a magnet by them. The fundamental physical cause of the percieved force is that when an electron must pass through these dipole pairs, it has to pass through a repelling negative charge and then a attracting positive charge.  The electron is attracted to the positive charge and it will tend to be deflected towards the positive charge as is shown in the diagram below in the upper left. This is the fundamental reason why we see charges deflect in a magnetic field. See this video showing how this deflection can work.

 

 

In the case of 2 parallel wires, the reason for the deflection is different because the electron is not passing through a positive/negative charge. Instead the electron is heading in the same direction as the dipoles are oriented so when the electron travels through the wire towards the right, it first sees a negative charge and then a positive charge. The electron would then be attracted to that positive charge and would veer towards the positive charge. However, if the wire is by itself, it will be surrounded by another set of dipoles on the other side of the wire which will also attract the electron with the same force. The opposing attractive forces cancel out and the net effect is that the electron is not deflected in the wire.

However, if there is another current carrying wire next to it, this this re-enforces and strengthens the dipole force between the two wires. The electron flowing through the wire sees unequal forces now and it veers toward the stronger dipole fields between the wires. As it does this, the electron cannot escape the wire, so it drags the rest of the wire with it and we see this as the attraction betwen 2 wires.This is shown as the top 2 wires in the diagram with current flowing in the same direction.

If you then consider a wire where the current is flowing in the opposite direction, then the dipoles are opposing each other and they cancel between the wires. Then the region of stronger dipole forces becomes the outside of the wires and the electron head away from the 2 wires and we see this as a repelling action between the wries.

This can be easily extended to how permanent magnets work. A permanent magnet works like a coil of wire wrapped around a nail. This creates a field which is similar to the straight wire except that it curves around. The dipoles are combed into a circular pattern, but the way the coils interact to create region of higher dipole strength works the same way to create an attraction or a repulsion.

The main difference is that in the magnet, they crystalization of the metal creates superconducting pathways through the crystal. Initially, there is no current flowing through these pathways. But when exposed to a strong magnetic fields, the electrons start to flow and find a path through the crystal so it forms a current loop. Once this current loop starts, it keeps going. Then each of the individual current loops re-enforce each other until they form a field which looks something like the coil of wire, although there are still some significant differences. Each tiny current loop can be thought of as interacting with another tiny current loop and together, they work in concert to create an overall attraction or repelling force

 

 

When you pass a wire between a North and South pole, it generates a current in a wire. The direction of the current depends on the direction that you are passing the wire through. We will consider the wire travelling from the bottom to the top of the diagram.  The diagarm shows a cross-section of the magnetic field between the magnets. The field is a circular polarization of the dipoles where the stronger dipoles are shown in bold in the center. The reason why a current is generated is because when an electron in the wire comes into the field from the bottom, it initially sees a force to the right (it is attracted to the positive charge). When it passes through the middle, it gets a double push to the right because on the left it is attracted to the big positive charge and on the right it is repelled by the big negative charge. As it goes past the middle, it sees a force to the left. This cancels out the initial force to the right, but does not cancel out the double push to the right provided by the center. Therefore, the electron sees a net force to the right and a current flows as the wire is passed through the magnetic field.

Solving Faraday's Paradox

An area that cannot be easily explaned by electromagnetic theory is unipolar induction. The problem seems to be best stated by this wiki page of the Faraday Paradox:

Here we have a rotating disk in a magnetic field and the disk generates a current from the axis to the outer edge of the disk. This all works perfectly fine with the Lorentz Force Law as you can see the electrons driven to the outer edge. This is mentioned as case 1. What's weird is that if you hold the disk and spin the magnets around, it generates no current. It would seem that the moving magnetic field is still cutting through the disk, so why isn't a current generated? Even weirder than that, if you spin both the disk and the magnets together so that there is no relative motion between them, this generates a current. How can it do this if there is no relative movement?
For case 1, the easiest way to view the homopolar generator is as a spinning disk between the poles of a magnet as is shown below. The disk is directly and completely centered between the poles of a magnet.:
According to my magnetic model, the field between the poles is circular and matches up in the direction and plane of the circular disk. This is very different from the conventional view that the magnetic field lines run between the N and S poles in a straight line. The key is that the magnetic field strength is strongest towards the center of the poles. When you spin the disk, the charges in the disk experience and uneven force as they pass by the line of weaker versus stronger dipoles in the center. I have shown this in the diagram below as bold plus and minus signs showing stronger field strength. They deflect into the direction of the strongest field strength which causes the electrons to migrate towards the center as the disk is spun clockwise and this is what actually generates the current between the rim and the axis as the mobile charges in the disk are attracted to the stronger field strength. If the disk were spun counter clockwise, the electrons would migrate outwards towards the rim and would cause a reverse current.

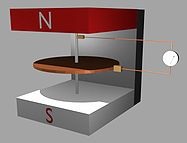
For case 2 the disk remains stationary, so the charges are not moving in any sense. What we do have is the magnet moving around the disk, but the magnetic field is only a stationary alignment of the dipoles. The alignment doesn't change because the true field lines are also circular. So rotating about the axis doesn't change anything. The dipoles themselves don't move with the rotating magnet. They are kept in their same relative positions as if the magnet were not moving. The charges in the disk aren't moving and neither are the dipoles, so we would expect no current to be generated in this situation. 

Conventional electromagnetic theory which defines the magnetic field lines as running through the disk would indicate that these fields lines which are at 90 degree angles to the disk must be cutting through the disk and must therefore be generating a force on the electrons through the Lorenz force. This is where the paradox comes in because the direction and shape of the magnetic field has been defined incorrectly.

For case 3 both the magnet and disk are spinning together. As I mentioned in case 2, the magnetic field doesn't change at all whether the magnet is moving or not. It is simply stronger in the center and weaker going out. However, in this case, the charges in the disk really are moving and they are cutting past the dipoles in the same was as in case 1, so in this case, we would also expect that a current will be generated.

Conventional theory would indicate that if the magnet and disk are moving together, then the field lines would remain stationary relative to the disk and so no current should be generated. Conventional theory cannot explain this and therefore it appears as a paradox.

However, this paradox can be solved. Once we understand the true nature and shape of the magnetic field , it becomes fairly obvious what is going on. Conventional theory has gotten the direction of the magnetic field lines completely wrong.

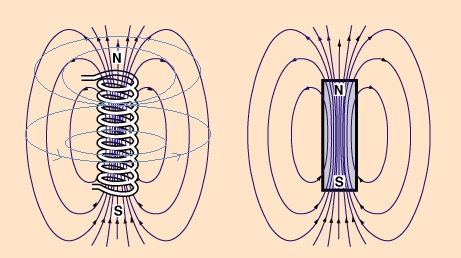
The diagram shows conventional field lines on the right. These define lines which point downward from the poles and form uniform vertical magnetic field lines between the N and S poles. This is wrong. The correct way to view the magnetic field line is that these field lines run in the same direction as the current that creates it which is shown on the left as light blue lines circling around the coil. This actually makes more sense that the field lines run in parallel to the current, not at a 90 degree angle to it.

To solve the paradox, one must recongize that the magnetic field doesn't change when you rotate the magnet around the axis since the real field lines are circular around the axis. So spinning about the axis makes no difference. Keeping the magnet stationary doesn't make any difference. The only thing that makes a difference is if the mobile charges in the disk are spinning and those are the cases where a current is generated. The paradox only arises if you think of the field lines as arrows connecting between the N and S poles of a magnet. Then you will have a big conceptual problem because spinning will definitely lead to magnetic field lines cutting through the disk which should generate a current, but they do not. 

In most cases, it doesn't matter that the magnetic field lines have been defined incorrectly. However, in the case of unipolar induction, it makes a great deal of difference. Redefining the magnetic field lines in this manner does not lead to a simple formula like the Lorenz force law, however, common electromagnetic interactions such as how 2 current carrying wires attract and repel and how current is generated when passing through a N and S magnetic field and how unipolar induction really works can be more easily explained. Therefore one needs to consider whether the field line direction and shape has been defined incorrectly.

 

 

\